Zeno van Elea is een Griekse logicus en filosoof die vooral bekend staat om de naar hem genoemde paradoxen. Er is niet veel bekend over zijn leven. De geboorteplaats van Zeno is Elea. Ook in de geschriften van Plato werd de ontmoeting van de filosoof met Socrates genoemd.
Rond 465 voor Christus e. Zeno schreef een boek waarin hij al zijn ideeën uiteenzette. Maar helaas heeft het onze dagen niet bereikt. Volgens de legende stierf de filosoof in een gevecht met een tiran (vermoedelijk het hoofd van Elea Nearch). Alle informatie over Elea werd beetje bij beetje verzameld: uit de werken van Plato (geboren 60 jaar later Zeno), Aristoteles en Diogenes Laertius, die drie eeuwen later een biografieboek van Griekse filosofen schreven. Zeno wordt ook genoemd in de geschriften van de latere vertegenwoordigers van de school voor Griekse filosofie: Themisty (4e eeuw na Christus), Alexander Afrodinsky (3e eeuw na Christus), evenals Philoponus en Simplicius (beiden leefden in de 6e eeuw na Christus). Bovendien zijn de gegevens in deze bronnen zo goed met elkaar in overeenstemming dat alle ideeën van de filosoof daaruit kunnen worden gereconstrueerd. In dit artikel vertellen we je over de paradoxen van Zeno. Dus laten we beginnen.

Paradoxen van de set
Sinds het tijdperk van Pythagoras werden ruimte en tijd uitsluitend vanuit het oogpunt van wiskunde beschouwd. Dat wil zeggen, ze werden verondersteld uit veel punten en punten te bestaan. Ze hebben echter een eigenschap die gemakkelijker te voelen is dan te definiëren, namelijk 'continuïteit'. Sommige Zeno-paradoxen bewijzen dat het niet in momenten of punten kan worden verdeeld. De redenering van de filosoof komt neer op het volgende: 'Stel dat we de verdeling tot het einde hebben voltooid. Dan is slechts één van de twee opties waar: ofwel krijgen we de minimaal mogelijke hoeveelheden of delen die ondeelbaar zijn, maar oneindig in hoeveelheid, ofwel zal deling ons leiden naar delen zonder omvang, aangezien continuïteit, die homogeen is, onder alle omstandigheden deelbaar moet zijn. Het kan niet deelbaar zijn in het ene deel, maar niet in het andere. Helaas zijn beide resultaten behoorlijk belachelijk. De eerste is te wijten aan het feit dat het splitsingsproces niet kan eindigen terwijl er onderdelen zijn die een waarde hebben. En de tweede is omdat in zo'n situatie in eerste instantie het geheel uit het niets zou zijn gevormd. ' Simplicius schreef dit argument toe aan Parmenides, maar het is waarschijnlijker dat de auteur Zeno is. We gaan verder.
Zeno's Paradoxes of Motion
Ze worden beschouwd in de meeste boeken die aan de filosoof zijn gewijd, omdat ze in onenigheid komen met bewijs van de gevoelens van de Eleatics. In relatie tot de beweging worden de volgende Zeno-paradoxen onderscheiden: "Arrow", "Dichotomy", "Achilles" en "Stages". En dankzij Aristoteles kwamen ze bij ons. Laten we ze eens nader bekijken.
Pijl
Een andere naam is de Zeno-kwantumparadox. De filosoof beweert dat alles stilstaat of beweegt. Maar er is niets in beweging als de bezette ruimte er in lengte gelijk aan is. Op een bepaald moment zit de bewegende pijl op één plek. Daarom beweegt het niet. Simplicius formuleerde deze paradox in korte vorm: “Een vliegend object neemt een gelijke plaats in de ruimte in, maar dat wat een gelijke plaats in de ruimte inneemt, beweegt niet. Daarom staat de pijl stil. ' Femistius en Phelopon hebben vergelijkbare opties geformuleerd.
"Dichotomie"
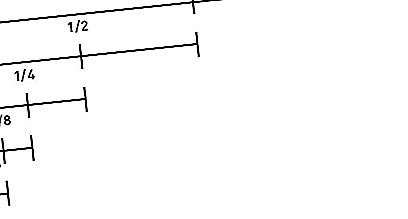
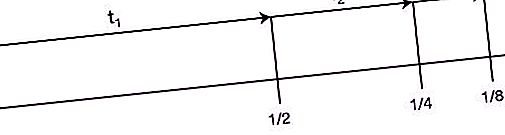
Staat op de tweede plaats in de lijst van "Zeno Paradoxes". Het luidt als volgt: “Voordat een object dat begint te bewegen een bepaalde afstand kan afleggen, moet het de helft van dit pad overwinnen, vervolgens de helft van het resterende enz. Tot in het oneindige. Omdat tijdens herhaalde delen van de afstand in de helft het segment steeds eindig wordt en het aantal van deze segmenten oneindig is, kan deze afstand niet in een eindige tijd worden overwonnen. Bovendien geldt dit argument zowel voor kleine afstanden als voor hoge snelheden. Daarom is elke beweging onmogelijk. Dat wil zeggen dat de hardloper niet eens kan starten."
Deze paradox gaf een zeer gedetailleerd commentaar op Simplicius, wat aangeeft dat in dit geval een oneindig aantal aanrakingen in een eindige tijd moeten worden gedaan. 'Iedereen die iets aanraakt, kan tellen, maar de oneindige set kan niet worden gesorteerd of geteld.' Of, zoals Philopon het uitdrukte, een oneindige verzameling is ondefinieerbaar.
Achilles
Ook bekend als de paradox van de Zeno-schildpad. Dit is het populairste filosofische argument. In deze bewegingsparadox doet Achilles mee aan een run met een schildpad, die aan het begin een kleine handicap krijgt. De paradox is dat de Griekse krijger de schildpad niet zal kunnen inhalen, aangezien hij eerst de plaats van zijn start zal bereiken, en zij zal al op het volgende punt zijn. Dat wil zeggen, de schildpad zal Achilles altijd voor zijn.
Deze paradox lijkt erg op een dichotomie, maar hier gaat de oneindige verdeling volgens progressie. In het geval van een tweedeling was er een regressie. Zo kan dezelfde hardloper bijvoorbeeld niet starten, omdat hij zijn locatie niet kan verlaten. En in de situatie met Achilles, zelfs als de hardloper begint te bewegen, zal hij nog steeds nergens komen rennen.
"Stage"
Als we alle paradoxen van Zeno vergelijken in termen van complexiteit, dan zou dit de winnaar zijn. Het is moeilijker dan andere om uit te leggen. Simplicius en Aristoteles hebben deze redenering fragmentarisch beschreven en men kan niet met 100% zekerheid op de betrouwbaarheid ervan vertrouwen. De reconstructie van deze paradox heeft de volgende vorm: laten A1, A2, A3 en A4 bewegingloze lichamen zijn van gelijke grootte, en B1, B2, B3 en B4 zijn lichamen van dezelfde grootte als A. B-lichamen bewegen naar rechts zodat elke B passeert En in een oogwenk, dat is de kleinst mogelijke periode. Laat B1, B2, B3 en B4 lichamen zijn die identiek zijn aan A en B, en beweeg relatief ten opzichte van A naar links en overwin elk van de lichamen in een oogwenk.
Het is duidelijk dat B1 alle vier de lichamen van B heeft overwonnen. Laten we voor een eenheid de tijd nemen die nodig was om één lichaam van B door één lichaam van B te laten gaan. In dit geval waren er vier eenheden nodig voor alle bewegingen. Er werd echter aangenomen dat de twee momenten die voor deze beweging voorbij waren minimaal waren en daarom ondeelbaar. Hieruit volgt dat vier ondeelbare eenheden gelijk zijn aan twee ondeelbare eenheden.